This is part two in a three-part series about designing multi-transfers flight routes and finding shortest paths with multi-objectives to be optimized. In the first post, I described how to load, clean and migrate the dataset from MySQL to Neo4j by populating the graph with Cypher query. The way you write the Cypher query will really depend on how you design your flight routes problem. The purpose of this second post is to show different ways to design the multi-transfers flight routes problem, that eventually lead to the final model that is satisying enough in term of both the easiness to do further analysis and the query time or performnance.

Different ways to model flights routes

Before starting to migrate entirely the MySQL database into Neo4j database, I started to do some experiments with a subset of the dataset to test the relevance of the design. Therefore I choose to populate the Neo4j database with flights data which don't have an inbound, that is, single way fights. These flights already contains trips that have many transfers, so it covers all the cases that we want to implement and covers the whole range of date (year 2017). After finding and designing the right and satisfying enough model, I migrate the entire dataset into Neo4j. The ultimate goal here, is to be able to design a graph which features relevant metrics that would be used similarly as weights and then applying a graph shortest path problem.

The 1st model: trip model

‌To build each model I use the Neo4j API (Python py2neo) and MySQL connector to fetch data from MySQL database in order to populate the Neo4j database by writing Cypher queries that create nodes, relationships and links then all together with additional properties.

The very first model was kind of straightforward, we just follow the way each trip is made, that is, I create the following unique nodes:

• City(green), Airport(red), Flight(blue)

and the following relationships:

• FROM(pink), links flight and the airport where the beginning of the trip starts
• TO(blue), links the last flight to the final destination airport.
• FROM_TRANSFER(yellow) and TO_TRANSFER(gray), similarly to FROM and TO, links in-between flights and airports.
• WAIT_FOR, links two flights between segments.
• HAS and IN are relationships that connects City nodes to Airport nodes (respectively one-to-many and one-to-one relationships).

Neo4j comes along with a web browser UI that allows to write query in a prompt and returns the visual result. The following figure shows a query that returns paths (limited at a given maximum nodes) from the airport PVG (Shanghai) to ICN (Seoul).

Figure 1 - The first model of the flight routes

All connected relationships here are given the departure and arrival date and time as properties.

This model has the drawback to be too complex, and contains too many relationships of different types. Simple queries will work fine, but complex queries will result in a difficult analysis.

The 2nd model: looping for the transfer

The second model will be a more simplified and understandable model where there are fewer different relationships. The following figure illustrates this second model for a query that searches for flights from CAN airport to whatever destination.

The query has found a result (limited to be easily visualizable) to two different destinations: ICN airport via one transfer at PVG airport, and to GMP airport via one transfer at SHA airport.

Figure 2 - Second model of flight routes, with WAIT loops

I change the previous FROM_TRANSFER and TO_TRANSFER, to a unifying FROM and TO respectively. After all, distinguish them doesn't bring any other advantages. Moreover, the previous WAIT_FOR relationship has been modified: instead of connecting two flights (the first and the second flights in a trip for example) it now "loops" on itself on an airport node. This is a natural way to think of, because one waits at an airport before joining the next flight, and the concept of looping on a node is quite popular in the graph modeling world. In this model, the price of each flight segment will be assigned as a property in the TO relationship, and the transfer time will be a property in the WAIT relationship.

However, before proceeding further analysis with this model, I notice one thing: in a query for searching paths from a source to a target node, Neo4j is not obligated to traverse a looping relationship. Therefore, for instance, from CAN to ICN via PVG the path that reaches ICN but going through the WAIT loop is considered as a path different from the one that won't go through the loop. This behavior is not suitable for our study because queries end up returning results that ignore the transfer and the associated waiting time, which is one of the main problem to solve in our study. Here's how the third model will fix this problem.

The 3rd model: the "go-straight" model

This model allows fix the problem of the loop that Neo4j might not traverse. The following figure illustrates this third model.

Figure 3 - Third model for the flight routes: TO and WAIT relationships have the same direction

Indeed, instead of looping, the WAIT relationship links, directionally, the transfer airport to the next flight. In addition, there will be only a single FROM relationship in a trip, connecting the very first flight to the origin airport. Afterward, there are only relationships that go straightforward to the destination airport, via TO relationship which contains the price metric (for the associated airports pair) in its properties, and the WAIT relationship that contains the duration metric in its properties.

However, the first, second and third model has one thing in common: the airports and flights nodes are unique. Relationships that link them together contain properties such as departure/arrival date and time. Between two nodes, there are thousands of relationships which contain these different dates which cover the whole year of 2017. Consequently, the query takes too much time to return. The next model fix this problem by introducing the concept of Day and Month nodes.

The 4th model: introducing Day and Month nodes

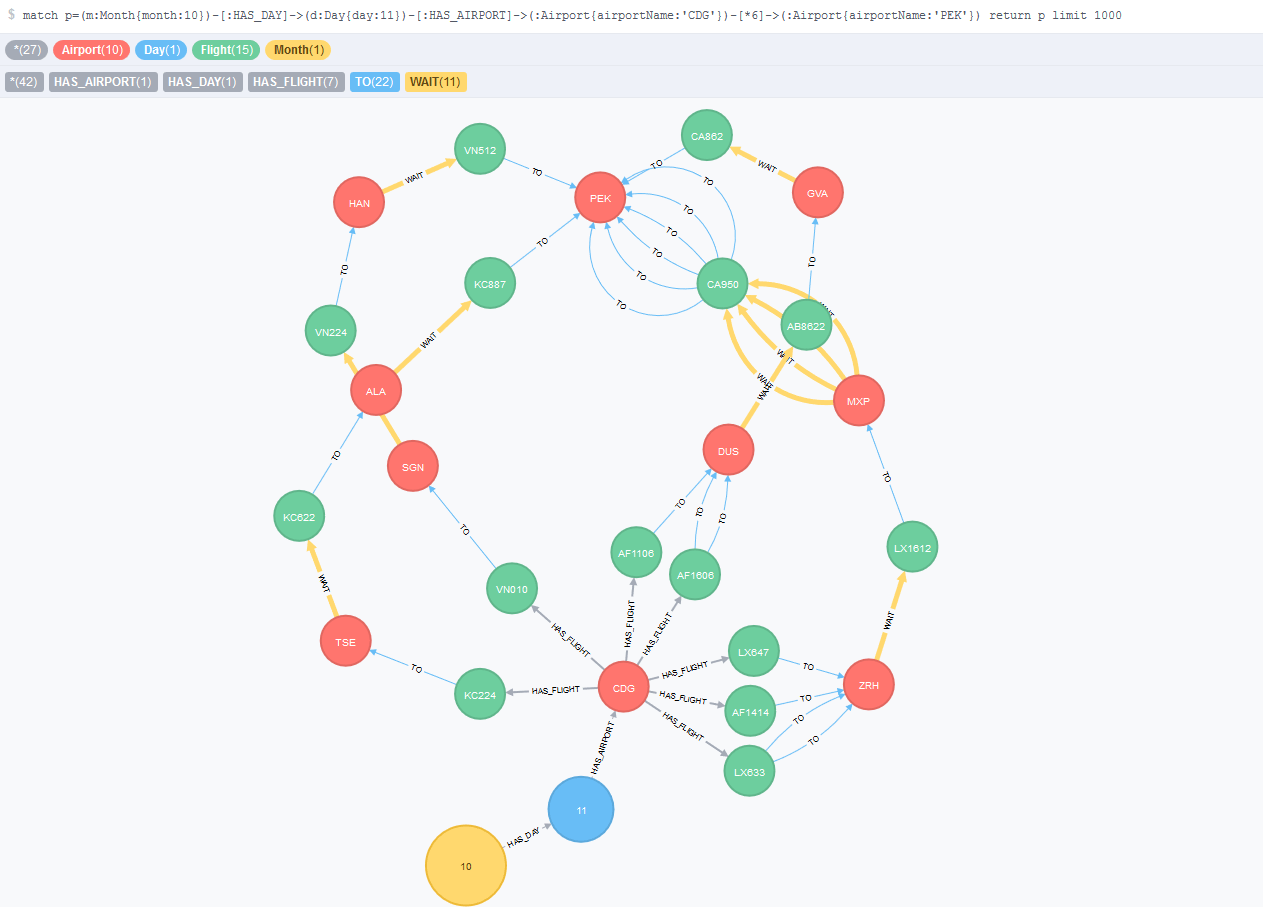
In the flight search problem, usually a user looks for flight at a specific date, or at least, within a specific range of dates. This model introduces the concept of Day and Month concept in order to filter out the unwanted dates within the searching date scope. In addition, I create non unique nodes associated to each day: there will be the same flights (in term of flight code) and airports (in term of IATA code, that is, the name of the airport in three upper-case letters) for each day. This will increase the number of total flights in the database but Neo4j is a scalable graph database that can handle billions of nodes. If we consider the entire dataset and not the subset for designing our model, we have a maximum of around 500 different airports 3000 flights each. This represent a total of around one million nodes in the entire year, which is a small number comparing to what Neo4j can handle. In addition there are other additional relationships types: HAS_DAY, HAS_AIRPORT, HAS_FLIGHT, and there is nothing longer the FROM relationship. The following figure illustrates this model for a query that looks for flights from to CDG (Charles De Gaulle) to PEK (Beijing) on the 11th of October, with up to two intermediate transfers.

Figure 4 - Fourth model that introduces the Day and Month nodes

The advantages with introducing Day and Month nodes, is that I only have to deal with nodes and relationships in the specific date specified in the Cypher query. This makes the query really fast since Neo4j starts by scanning not the entire nodes and relationships objects, but only those with the corresponding date and month. The way that Neo4j seek for the matched nodes given a query, can be described by using the PROFILE keyword before a query. For our previous example, here are the steps before reaching to the result:

Figure 5 - Execution plan of the query

This shows the number of the database hit, that is, when the Neo4j have to "touch" the database to find the matched nodes. Here we can see that the database was hit only 3700 times in 7ms, the greater the number of database hits, the more the query takes time. The result of the query is almost displayed instantly. This hit number is small compared to the previous models that reached dozen of millions hits and can be explained because only airports that "belong" to the specific date in the query, are touched, filtered out the others, therefore only fights connects to these date-specific airports are touched. This method leaves the other nodes untouched, speeding then the query time. This model, satisfying enough, however lacks one thing that the next and final model compensate.

The final model: finding hidden connectable flights

The previous (4th) model is satisfying the modeling flight routes enough, but all the previous model have one thing in common: they follow the data inside the dataset. Indeed, the WAIT is created based on whether or not the trip has a transfer. This final model defines a way to find all hidden possible connection between flights and airport. To do so, this model completely delete the WAIT relationship and instead, keep only four relationships: HAS_DAY, HAS_AIRPORT, HAS_FLIGHT and TO.

By doing this, I won't constraint the database by only populating fights and airports based on the data inside the MySQL database. It generalizes all the routes, and do not distinguish those with transfer with those without transfers. The following figure illustrates this model for a query from SHA airport to CDG on the 11th of February with up to two transfers.

Figure 6 - Final model of flight routes that enables finding hidden connectable flights

By generalizing the relationships types, I lose the information of the transfer time within the previous WAIT relationship property, and instead, I calculate, this transfer time based on the difference between the arrival time of the segment n, and the departure time of the segment n+1. This calculation is done later in the analysis part by analyzing the results returned by the query. So, the transfer time is an implicit weight that is not present explicitly in our graph, but is calculated afterward.

The query time is similar to the 4th model, and with this model flights that constitute a whole trip, are treated as an independent entity that can be connected to others flights from other trips to form new possible trips with different combinations of departure/arrival time and prices.

I keep for the next analysis sections this model. The purpose of the analysis part will be described in the next post is to find valid routes amongst all the connectable flights within a specific day. Indeed having connectable flights doesn't mean that all connectable are valid: valid routes are routes where the chronological order between arrival time of segment n and the departure time of segment n+1 is respected.

For the complete code, please check my GitHub repository.